上节的索引组织表，具体是使用什么索引算法，把数据给组织起来。

即，需要什么数据结构，便于搜索这条索引里的数值。

一、本章内容

介绍主流的索引查找算法，最终引出主角：B+树。

二、主流的索引查找算法

2.1 6个

• 线性查找：Array数组、Linked List链表。从头开始，一个一个找。
• 二分查找：可以视为线性查找的升级。即可以使用线性查找的数据结构，但是查找算法不一样
• 二叉树：效率更高，但是存在平衡问题。
• 平衡二叉树：解决了平衡问题。不足：以上所有四种，一个节点只能存放1个数据，磁盘利用率低。
• B 树：一个节点只能存放不只一条数据。但是也存在平衡问题。
• B+ 树：解决了上面的平衡问题。B+ 树，可以理解为B树、线性查找的结合。

2.2 线性查找 Linear Search

1.原理

本质：一个一个查找。

2.试验

优质网站，动图演示，演示原理：

Google浏览器： usfca，数据可视化，就能搜到以下大学（旧金山大学），创建的数据结构可视化平台：

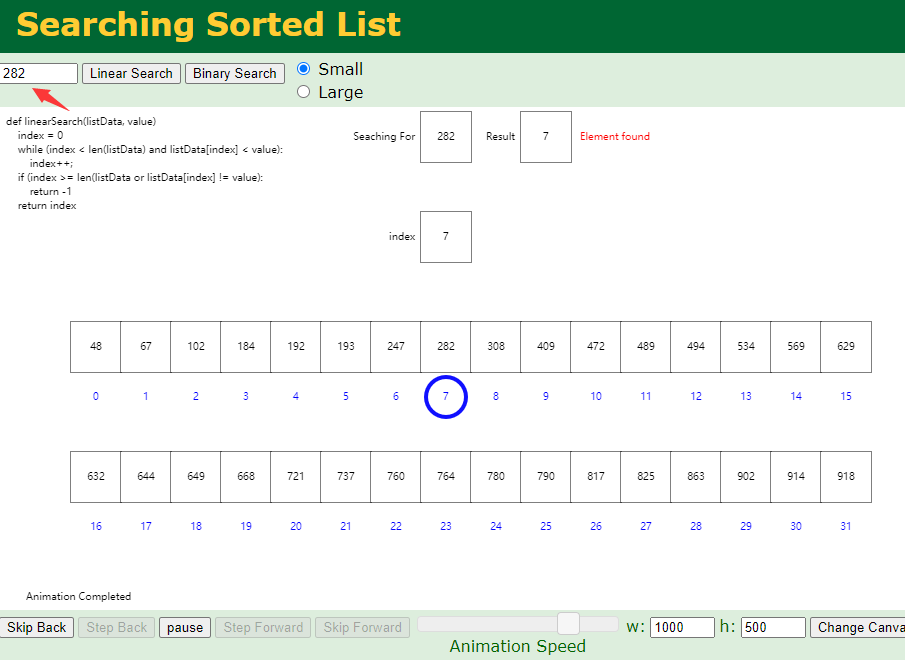
一个框代表的是一行数据，显示出来的只是id。比如数据的主键是48，id是48.

线性查找，id为282的数据：从左开始，逐个比较：

2.3 二分查找 Binary Search

1.原理

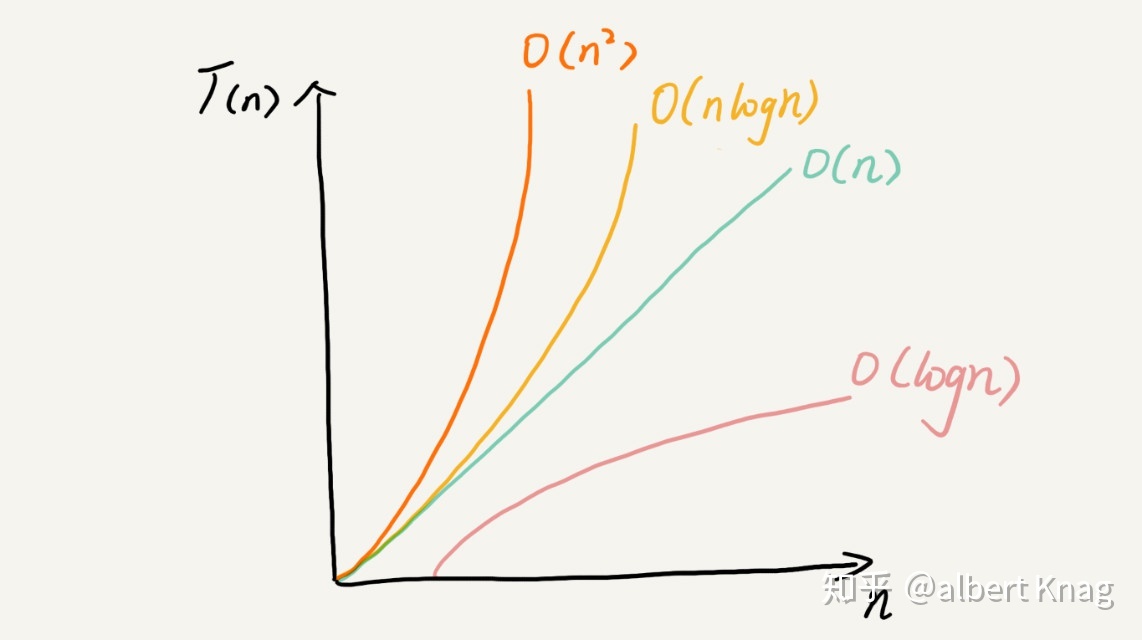
虽然N很大，但是前面加个log，最终结果就会减小的非常小。

这样，就算你N数据量剧增，logN也不会增加太多。

上图来自：https://www.zhihu.com/tardis/landing/yidian/ans/148670878

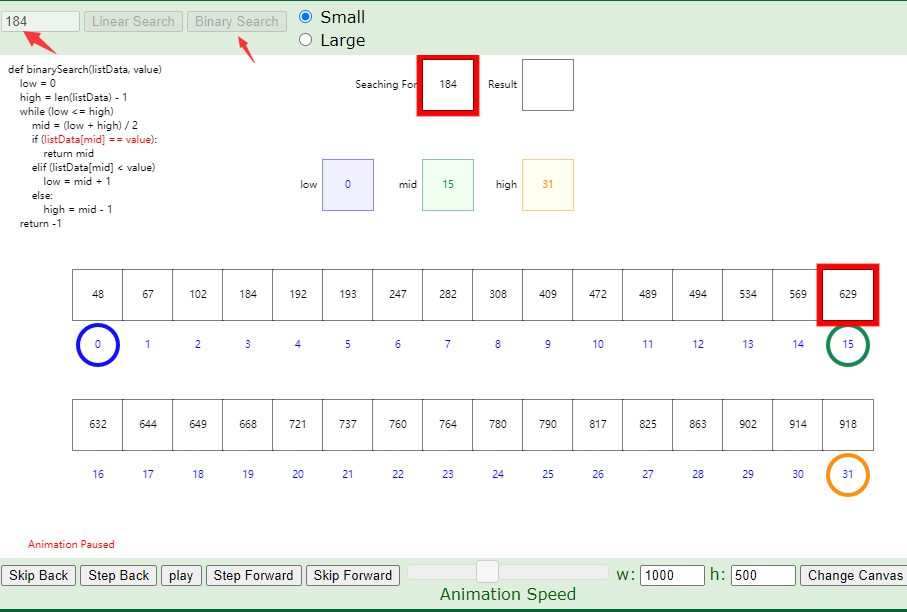
不足：必须知道和获得这段数据的中点位置。但有时拿不到：比如磁盘随机读写时，一个表中的100万个id数据，并不是连续读写的，因为磁盘是碎片化的。

2.试验

因为上节的线性查找，效率低。所以，诞生了二分查找。

2.4 二叉树 Binary Tree

基于上节二分查找树的不足，所以又诞生了二叉树。

1.原理

• 时间复杂度，跟二分查找一样。天然的被根节点分成了左右两个子树，前一半、后一半。即，满树，跟二分查找效率相同。

• 缺陷：不平衡

  在如下试验部分：新增的数据，id越来越大时，会变成一个链表，即退化成线性查找O(N）。树的优势丧失。

2.试验

二叉树，搜索是从最上面的根节点开始的。

比如：查询id为10：

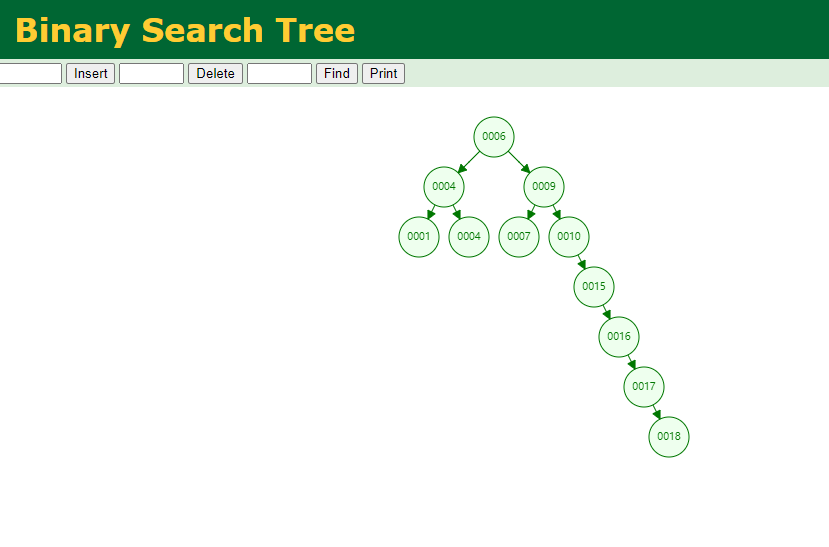
二叉树的不平衡的缺陷，导致退化为链表：

当插入的数据，越来越大时：

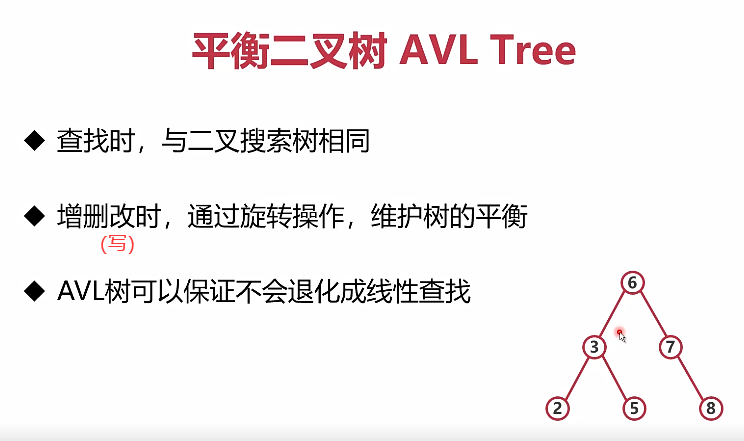
2.5 平衡二叉树 AVL Tree

1.原理

• 能通过左旋、右旋，确保树永远平衡，不会让树的一边特别长，退化成链表

2.试验

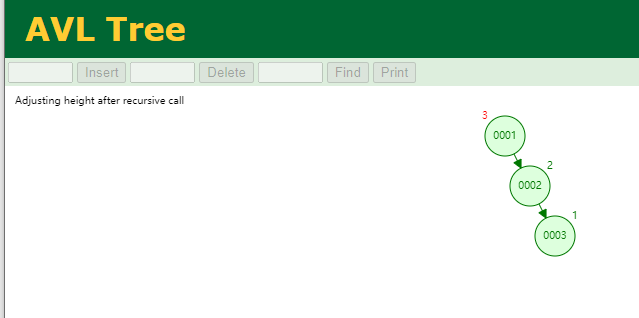
分别插入id为1、2、3：

自动的左旋：

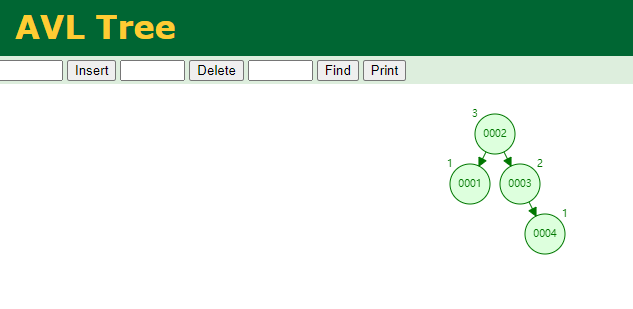
再插入id为4：

再插入id为5：

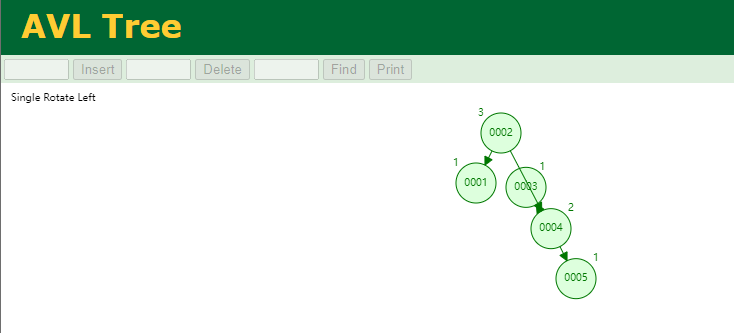
因为右子树特别长，所以左旋如下：

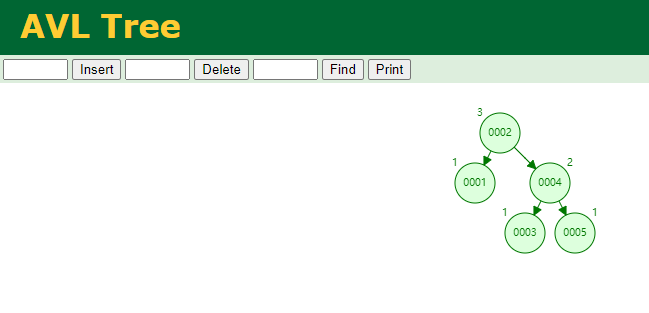
左旋的规律：

加上叶子节点，

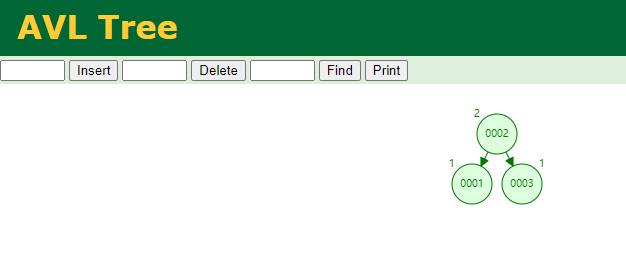
如果是2个，没问题；

如果是3个，那么就左旋，把中间那个节点，提起来。

三、B 树

接下来，介绍B树、B+树是怎么诞生的。这是为后续介绍B+树应用在InnoDB存储引擎，做铺垫。

3.1 平衡二叉树的致命缺陷

平衡二叉树，各方面性能优良。为什么数据库没有用它作为索引的数据结构呢？

致命缺陷：1个节点，只能包含1条数据。

因为硬盘，都有一个最小读写单位。

比如：机械磁盘：最小是512B

SSD：最小是4K。

如果一般，数据库中普通的1条数据都很小。你存储的东西往往不足上述最小单位，要么你和别的数据凑一块，放进去；要么就只放小小的你。

这会导致前者更混乱复杂，不容易查找，后者浪费空间。

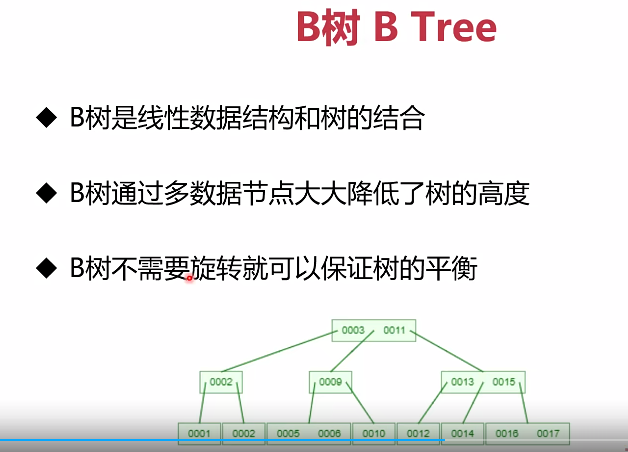
3.2 B Tree的定义

1.

基于不足，在平衡二叉树基础上，所以就诞生了一种新的数据结构：B Tree。

1个节点，能放多个数据。

好处：

• 硬盘利用率高：可以把id为1-10的数据，全部放在1个节点上。这样就能占满硬盘的最小存储单位（实际是，成为最小单位的倍数）。
• 一次就能存储多数据，能减小硬盘的读写频率。之前是1次读1行，现在是1次读10行。

B Tree中的B是什么意思？

B是发明人的姓，跟二叉树Binary Tree没有任何关系。

有人说这个B是平衡，我的理解不是。因为B Tree是在平衡二叉树 AVL Tree基础上进化而来，后者就已经是平衡的了。：）

3.3 B Tree的特点：AVL Tree+线性结构

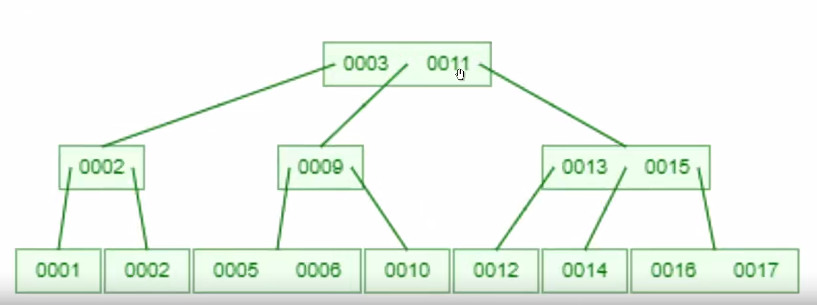
• 根节点有2条数据，有3个指针（下面的0003前面还有一个小数据结构，用于指向的）
• 在节点内，是单链表，线性查找
• 在节点外部，是树，是对数阶

原则：树的高度，能降低就降低。每个节点存放的数据，越多越好。

就算是SSD硬盘，其速度也是远低于内存的。

所以应该是从硬盘上把这个节点的所有数据全部取出来，放到内存，进行遍历。而不是直接在硬盘里，遍历去找。

3.4 B Tree的缺陷：范围操作效率低

范围操作，太麻烦，效率很低。

查找一段数据，5-9，即5、6、7、8、9，每次都要回根节点来查找：

数据库中有大量的范围查找：

• 查找10岁-18岁之间的人
• 查找身高在1.5m-1.6m之间的人

四、B+树

4.1 特点（B树+链表）

1.改进

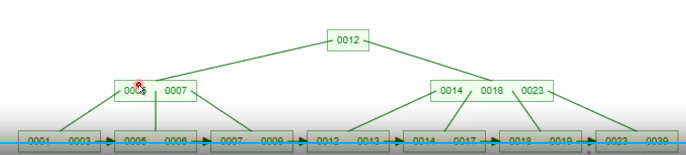
（1）所有的数据，都集中放（"落"）在了最下面的叶子节点里

除了叶子，上面的都是索引（指针），提供寻找功能

（2）叶子节点之间，用箭头形成了链表

即线性表，可以保证范围查询时，效率极高

2.图示

比如，还是查找一段数据，5-9，即5、6、7、8、9，不用每次都要回根节点来查找，只需要通过线性遍历的方式就能快速找到后面的连续数据：

图：

五、小结

重点不是B+树的更新、删除等操作，而是B+树，这个新技术，是怎么发展而来的。

只有了解一个技术的前因后果，才能在以后的创新上有自己的见解。

• 不只是InnoDB，MyISAM，PostgreSQL，或是NoSQL数据库，都是以B+树为基础的

很多时候，都会说从0到1的创新：其实，这很少。

大部分的创新，是1+1>2

B+ 树，就是典型的例子。因为结合了二叉树、B树、线性表，取其所长。